Innehållsförteckning
”Kursens viktigaste samband”
pV-diagram dieselmotor
Termodynamikens andra huvudsats: entropi, maxwells demon
Carnot process
Exempel: Hämta energi, Olika tillståndsändringar, Volymändring för antändning av papper
”Kursens viktigaste samband”
pV-diagram dieselmotor
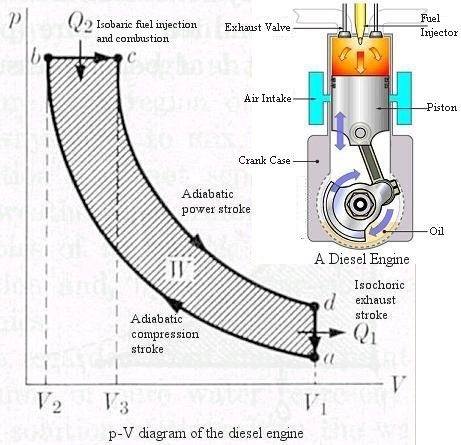
(
)
Verkningsgrad:
Termodynamikens andra huvudsats
- Isolerat system
- Oordningen blir aldrig ordning
Entropi
- Mått på oordningen
Maxwells demon
- Två kärl
- Ventil som endast släpper igenom varma (snabba) molekyler från ena kärlet till andra
- Minskad entropi i behållaren
- Ökad entropi till omgivningen.
Carnot process
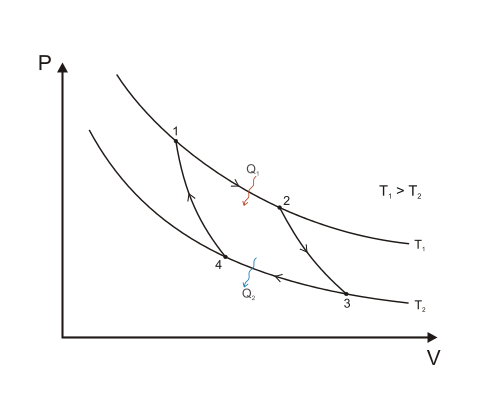
Ex.: Hämta energi
Du har en cylinder med kolv och får i uppdrag att gå ut och hämta värmeenergi. Det är kallare ute än inne ()
- Hur gör du?
- Hur gör du med minsta möjliga arbetsinsats?
Ex.: Olika tillståndsändringar
För att se vilken typ av tillståndsändring det rör sig om är det bra att jämföra hur processen sett ut i ett pV-diagram.
- Varmluftsballong – isobar (volymen ökar lite, temperaturen desto mer)
- Öppna en burk kolsyrat vatten – adiabat (snabb tillståndsändring, utan värmeöverföring)
- Pumpa ett bildäck – isokor (volymen ändras ej, dock temperaturen något och givetvis trycket)
- Sänka en ballong i en pool – isoterm (det blir en långsam tillståndsändring där värmen hinner överföras)
Ex.: Volymändring för antändning av papper
- Antändningstemperatur papper:
- Tryck:
- Initial temperatur:
- Processen är en adiabat.
- Vilken volymändring behövs?
Lösning
- Volymändringen:
,
- Skriv in
-värdet i ovanstående ekvation och få ut
- Insatt i (1) ger 1-0,28=0,72=72%
Film som visar exemplet: Fire Syringe, Youtube