Innehållsförteckning
Fasdiagram, ideal fluid, kontinuitetsekvationen, allmänna strömningslagen, bernoullis ekvation, venturirör, pitotrör, toricellis teorem, mariotte flaska, viskositet, poseulles formen, reynolds tal
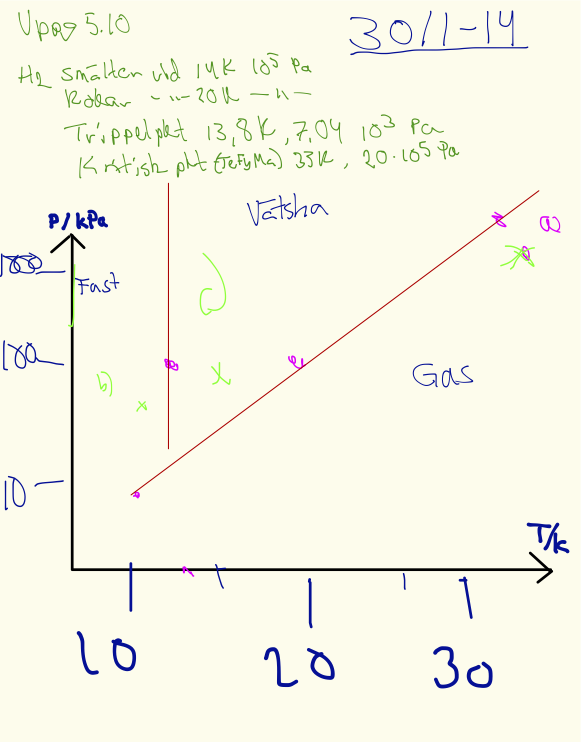
Uppgift 5.10
Rita ett fasdiagram för
Lösning
- Smältpunkt: 14 K, 10^5 Pa
- Kokpunkt: 20 K, 10^5 Pa
- Trippelpkt: 13,8 K, 7,04*10^3 Pa
- Kritisk punkt: 33 K, 20*10^5 Pa
Hydromekanik
Fluid: Strömmande gas eller vätska
Ideal fluid
(Modell)
- Inkompressibel
- Ingen viskositet
- Laminär strömning
Ekvationer
Kontinuitetsekvationen
Allmänna strömningslagen
Bernoullis ekvation (för ideal fluid)
Olika sätt att mäta
Venturirör
Strömningshastighet (i t.ex. vattendrag)
Pitotrör
Tryck (fart, t.ex. flygplan)
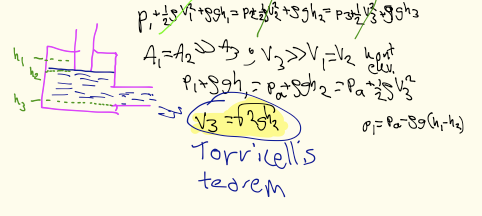
Torricellis teorem
”Samma uttryck som om det vore en boll”
Mariotte flaska
Viskositet
”Bromsande kraft”
Laminär strömning i rör
Drivande kraften: friktionskraften
Poseulles formel
Reynolds tal
- Re < 2000: Laminär
- Re > 4000: Turbulent