Ex.: Blodtryck. Ex.: Bolmenanläggningen. Ex.: Eka.

Termodynamik: frihetsgrader, tillståndsändringar (isoterm, isobar, isokor och adiabat), Termodynamikens första huvudsats. Arbete, värme, $latex C $, inre energiändring,

Exempel: Blodtryck

• Äldre person: 180/110
• I ungdomen: 120/90

a) Vad är enheten?

b) Uppskatta hur många procent blodomloppets ’rörradie’ har minskat? Antag: oförändrat flöde.

Lösning

a) Enheten är mmHg

b) Poissons ekvation: $latex \phi =\frac{\pi}{8\eta}\cdot \frac{p_1-p_2}{L}R^4 $

1. Antar att den gamla radien är $latex x\cdot R$.
2. Då oförändrat flöde förutsätts innebär att: $latex \phi_{ung}=\phi_{gammal} $
3. Sätter $latex \alpha=\frac{\pi}{8\eta}\cdot \frac{1}{L} $. Detta då $latex \alpha$ är konstant för båda åldrarna. 
4. Den nya ekvationen lyder alltså: $latex \phi_\alpha=\alpha\cdot (p_1-p_2)\cdot R^4$
5. $latex \phi_{\alpha,ung}=\phi_{\alpha,gammal}\Leftrightarrow \alpha \cdot 30\cdot R^4=\alpha \cdot 70(xR)^4 $
6. $latex 1=\frac{3}{7x}=0,81$
7. Svar: 19%

---

Exempel: Bolmenanläggningen

Dricksvatten från en sjö i Småland till Lund.

• Längd, $latex L=80km$
• Höjdskillnad, $latex h=90m$
• Area, $latex A=8m^2$
• Flöde, $latex v=2,5m^3/s$

a) Är flödet laminärt eller turbulent?

b) Vad är tryckfallet p.g.a. friktionen?

Lösning

a) Använder Reynolds tal: $latex Re=\frac{\rho Vd}{\eta}$.

1. Räknar ut rörets diameter: $latex A=\pi R^2=8m^2\Leftrightarrow R=1,6m \Leftrightarrow d=3,2m$
2. Räknat ut hastigheten för fluiden: $latex \phi=vA=2,5m^3/s \Leftrightarrow v=0,3m/s $
3. Vet att $latex \rho=10^3$, $latex \eta=10^-3$
4. Sätter in i ekvationen för Re: $latex Re=\frac{10^3\cdot 0,3\cdot 2\cdot 1,6}{10^-3}=9,6\cdot 10^5 $
5. Turbulent eftersom $latex Re > 4000 $

b) Använder sambandet: $latex p_1-p_2=2f\frac{L}{R} \cdot \frac{\rho v^2}{2}=f\frac{L\rho \phi^2}{\pi^2\cdot R^5}$. Antar skrovlig yta (påverkar tabelvärdet $latex f $)

1. $latex \Delta p=2\cdot 0,7\frac{8\cdot 10^4\cdot 10^3\cdot 0,32}{1,6\cdot 2}=3\cdot 10^5 Pa$
2. Svar: Tryckfallet p.g.a. friktionen är $latex 10^5 Pa$

Bonus: Behöver vattnet pumpas?

1. $latex \Delta p_{niva}=\rho g h = 10^3\cdot 9,81\cdot 90 \approx 9\cdot 10^5 Pa $
2. $latex \Delta p_{niva} > \Delta_p$ så det behövs ej pumpar.

---

 Exempel: Eka

Eka förtöjd. Strömningshastigheten ökar p.g.a. regn.

• Längd, $latex L=2,5 m$
• Bredd, $latex b=0,6 m$
• Höjd, $latex h=0,4 m$
• Massa, $latex m=75 kg$

Antagande

• Vattnet: ideal fluid
• Ok använda Bernoullis ekvation.

a) Beräkna ekans djupgående (dvs. avståndet mellan botten och vattenlinjen) innan vattnets strömningshastighet ökar.

b) Vid vilken strömningshastighet i vattenfylls ekan (dvs. djupgåendet = höjden = -0,4 m)?

Lösning

• Väljer vattenytan som referenslinje, dvs. då $latex y=0$. Detta innebär att botten befinner sig på $latex y=-0,4$
• På ekan verkar ett tryck $latex P=P_{atm}+\frac{F}{A}=P_{atm}+\frac{mg}{L\cdot b}$
• Lägger ut tre stycken referenspunkter

1. 1. Botten på ekan, lugnt vatten
   2. Botten på ekan, strömmande  vatten
   3. Ytan på ekan, strömmande vatten

• Hastigheten är lika på botten och ytan i det strömmande vattnet: $latex v_2=v_3=0$ (ty båten står still)
• Bernoullis ekvation: $latex p_1+\frac{1}{2}\rho v_1^2+\rho g y_1=p_2+\underbrace{\frac{1}{2}\rho v_2^2}_{=0}+\rho g y_2=p_{atm} $. Där $latex p_{atm}$ är atmosfärstrycket
• $latex p_1=p_2=p_{atm}+\frac{mg}{A} $

a)

1. $latex p_2+\rho g y_2=p_{atm} $
2. $latex p_{atm}+\frac{mg}{A}+\rho g y_2=p_{atm}\Rightarrow y_2=\frac{m}{A\rho}=\frac{75 kg}{2,5m\cdot 0,6m\cdot 10^3 kg/m^3}=0,05m$
3. Svar djupgåendet är 0,05.

b)

1. Genom att använda positionerna (1) och (2) fås: $latex \frac{1}{2}\rho v_1^2+\rho g y_1=\rho g y_2\Rightarrow v_1=\sqrt{2g(y_2-y_1)}=2,6m/s$

---

Termodynamik

Tryck: $latex p=\frac{2}{3}n_0(W_{kin})_{en} $

Kinetisk energi, ideal gas: $latex (W_{kin})_{en}=\frac{3}{2}kT$. ($latex k=1,380650\cdot 10^{-23}J\cdot K^{-1}\cdot stycken^{-1} $).

Frihetsgrader

• Behövs för att kunna beräkna $latex W_{kin} $.
• I rummet: 3 frihetsgrader.
• Ädelgaser: 3 frihetsgrader.
• Varje frihetsgrad ger: $latex W_{kin}=\left( \frac{1}{2}kT \right )\cdot \text{antal frihetsgrader} $.
• Molekyler (av flera atomer) kan även vibrera och rotera vilket ger minst tre frihetsgrader för en gas.

Tillståndsändring

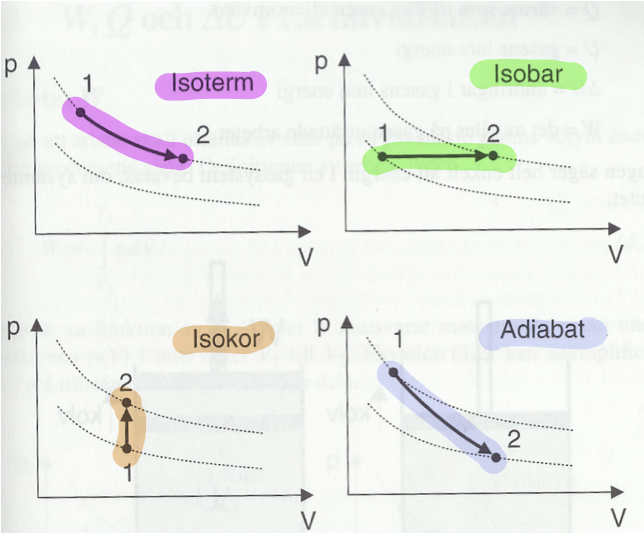
• Isoterm => konstant temperatur ($latex \Delta T=0$)
• Isobar => konstant tryck ($latex \Delta p=0$)
• Isokor => konstant volym ($latex \Delta V=0$)
• Adiabat => ingen värmeförändring ($latex \Delta Q=0$)

Termodynamikens första huvudsats

$latex \underbrace{Q}_\text{Tillford varme}=\underbrace{\Delta U}_\text{Andring av inre energi}+\underbrace{W}_\text{Utfort arbete} $

• $latex Q>0\Leftrightarrow \text{Systemet tillfors varme}$
• $latex \Delta U=\text{Slutenergi}-\text{Startenergi} $
• $latex W>0\Leftrightarrow \text{Systemet utfor arbete}$

Arbete

$latex dW=p\cdot dV $

Värme

$latex Q=mc\Delta T=\frac{m}{n}cM\Delta T=nC\Delta T$

• Molar specifik värmekapacitet: $latex C=cM $
• (För gaser används oftast $latex Q=nC\Delta T$)
  

Två olika $latex C $ (isokor/isobar)

• Isokor: $latex C_v $, $latex W=0$
• Isobar $latex C_p$, $latex W>0$
• $latex C_p>C_v$. (För isobar blir del av $latex Q$ $latex W$)

Inre energiändring

Ideal gas: $latex W_{pot}=0$. Inre energin helt beroende av $latex T$.

$latex \Delta U=\frac{f}{2}Nk\Delta T=n\frac{f}{2}R\Delta T $

• $latex U $ är inre energiändringen
• $latex f $ är antalet frihetsgrader (enatomig gas och ädelgaser: $latex f=3 $)
• $latex O_2,N_2:f=5$ om $latex 50K<T<2000K$

$latex C_v=\frac{f}{2}R$

$latex C_p=\frac{f}{2}R+R$

$latex \gamma=\frac{C_p}{C_v} $

	Isokor	Isobar	Isoterm	Adiabat
$latex Q$	$latex \frac{f}{2}nR\Delta T$$latex nC_v\Delta T$	$latex \left( \frac{f}{2}+1\right) nR\Delta T$$latex nC_p\Delta T$	$latex Q=W $	0
$latex \Delta U$	$latex \frac{f}{2}nR\Delta T$	$latex \frac{f}{2}nR\Delta T$	0	$latex \frac{f}{2}nR\Delta T $
$latex W $	0	$latex p(V_2-V_1) $$latex nR\Delta T$	$latex nRT\ln \left( \frac{V_2}{V_1} \right )$	$latex -\Delta U $